Bimetal: Definition, Properties, and Applications
Many domestic, commercial, and industrial processes rely on thermostatic bimetals for electrical or mechanical actuation applications. They can be found in many control switches such as early thermostats, clocks, circuit breakers, and electrical appliances.
What is a bimetal?
A bimetal or thermostatic metal is a sheet or strip of two or more composite materials having different coefficients of linear thermal expansion bonded by riveting, brazing or welding. The material with the larger coefficient of thermal expansion (CTE) is considered as the active component, and that of smaller CTE is the passive component. The active component usually has alloys containing iron, manganese, nickel, or chrome in varying amounts. Whereas on the passive side, invar is often chosen, an iron-nickel alloy containing 36% nickel. Some bimetals include a third layer of copper or nickel in between the active and passive sides in order to increase thermal conductivity and decrease the material’s electrical resistivity [1, 2].
Properties of bimetal
Bimetals work with the propensity of metals to expand when heated, and contract when cooled. The resulting change of curvature, or bending, in response to temperature change, is a fundamental property of all thermostatic bimetals. In effect, the temperature change is converted into mechanical displacement. The behaviour of bimetals is predictable and repeatable. The components used for bimetals are selected for their temperature characteristics as well as their thermal conductivity, stability, strength, workability, and electrical properties.
Flexivity
The fundamental characteristic of a bimetal is flexivity, also known as specific curvature. It is an important property of bimetals that is defined by the curvature change along its longitudinal axis. This is expressed as [3]:
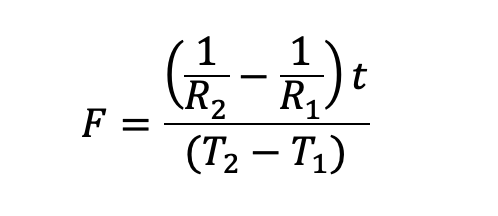
where,
F = flexivity (°F-1) (SI: °C-1)*
R2, R1 = radii of curvature of the active and passive sides, respectively (in) (SI: mm)
T = thickness of the strip (in) (SI: mm)
T2, T1 = temperatures (°F) (SI: °C)
* This simply represents the SI unit once mathematically converted from the standard system. It is not a standard unit. It follows similarly throughout the text unless stated otherwise. See ASTM Designation B106.
And for a simple beam:
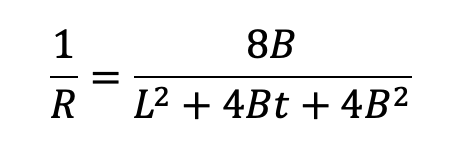
where,
L = distance between support points (in) (SI: mm)
B = movement (in) (SI: mm)
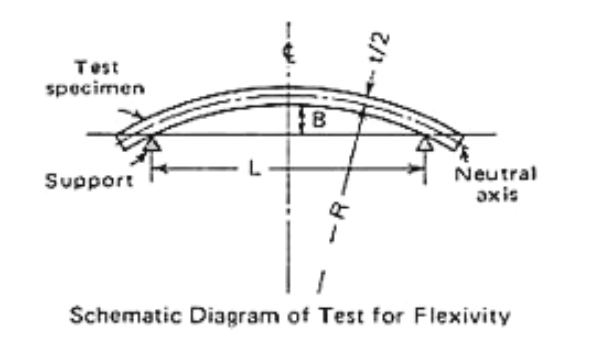
Image 1: Schematic Diagram of Test for Flexivity. Retrieved from Ref. 3
Radius of curvature
Moreover, the equation below shows the flexing or radius of curvature of a bimetal strip. Here, we can see the factors that influence the bimetal bending and its relationship [3]:
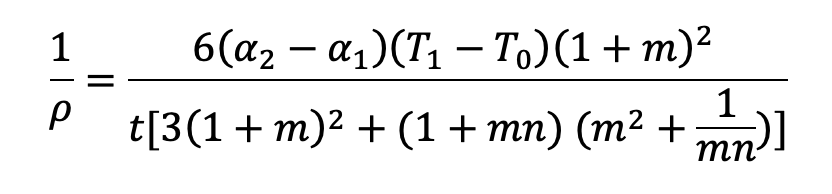
where,
ρ = radius of curvature of the strip (in) (SI: mm)
α1 = first strip coefficient of expansion (°F-1) (SI: °C-1)
α2 = second strip coefficient of expansion (°F-1) (SI: °C-1)
T0, T1 = temperatures (°F) (SI: °C)
E1 = modulus of elasticity for first strip (psi) (SI: Pa)
E2 = modulus of elasticity for second strip (psi) (SI: Pa)
t1, t2 = thickness of each component (in) (SI: mm)
t = thickness of the bonded strip (in) (SI: mm)
n = E1/E2
m = t1/t2
This equation shows that the thermostatic bimetal bending is directly proportional to temperature change of the component strips and the difference in the CTE, and inversely proportional to the thickness of the combined strips. The radius of curvature is also affected by the thickness ratio and the ratio of the moduli of elasticity of the two strips.
Electrical resistivity and thermal conductivity

For applications where heat is generated by passing an electric current through a bimetal, knowledge of the electrical resistivity and thermal conductivity as parameters for temperature change is important. This is true for many bimetals that are used as circuit breakers. For a resistor, the equation below shows how temperature rise can be derived [3]:
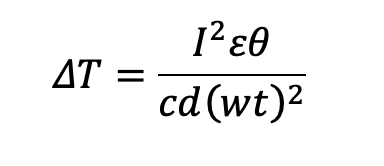
where,
ΔT = temperature rise (°C)
I = current (A)
ε = electrical resistivity (µΩ)
θ = time (s)
c = specific heat capacity (J/g°C), estimated at 0.502 for all Bimetals
d = density (g/cm3)
w = width (mm)
t = total thickness (mm)
By using the convenient conversion factors, a similar formula can be derived in English units.
Bimetal applications
Temperature indication
Bimetals are used for temperature indication as in the spiral or helix actuated pointer thermometers. Such thermometers help measure temperatures in offices, refrigerators, and even on aircraft wings. The bimetals of this type are usually 0.005 in (0.127 mm) to 0.015 in (0.381 mm) thick, and the coil is fitted to the pointer scale as it generates sufficient torque in order to move the pointer freely. The temperature range covered by bimetals extends approximately between -50°F and 1000°F (-46°C and 538°C). Angular deflection rate is usually at 2.5-3° per degree Fahrenheit [4].
Temperature control
Bimetals are utilised as a means to control the temperature, as in room temperature thermostats. In such devices, a bimetal blade holds a current-carrying contact point that is linked to a coupled static contact point. This allows for the automatic switching of circuits to control heating and cooling of electrical devices as the blade arches when a certain temperature is reached [4].
Tube and pipe couplings
For cryogenic, non-magnetic, and nuclear applications where metal properties must be switched reliably, bimetallic couplings are used to enable direct connection and transition for pipes and tubes with different CTEs. These fittings may also be used in other thermal transfer applications [4].
Function Control
By introducing heat to a bimetal – or what is known as auxiliary heating – the function of a device containing the bimetal can be controlled. Circuit breakers and time delay devices are examples of these devices. Relative functions such as current and time can be controlled by installing the bimetal piece as the active element in the device [4].
Sources
[1] (2018) Bimetals. Electrical4U. Retrieved from: https://www.electrical4u.com/bimetals/
[2] (2008) KANTHAL Thermostatic Bimetal Handbook. Retrieved from: https://www.ibt.co.il/uploaded_files/documents/Kanthal_Thermostatic_Bimetal_U3743.pdf
[3] (n.d.) Thermostatic Bimetal Designer’s Guide. Engineered Materials Solutions. Retrieved from: https://www.emsclad.com/fileadmin/Data/Divisions/EMS/Header/Bimetal_Desingers_ Guide.pdf
[4] (1942) Howard, E. R. Thermostatic Bimetal. Engineering and Science, 5 (4). pp. 16-24.