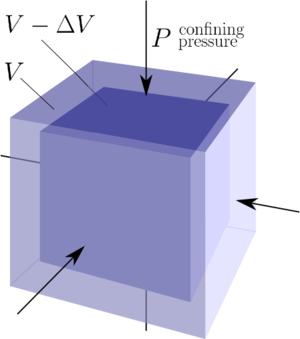
What is Bulk Modulus?

The bulk modulus of a material is the ratio of volumetric stress to volumetric strain. It is not to be confused with Young’s modulus, the ratio of tensile stress to tensile strain, or with shear modulus, the ratio of shear stress to shear strain. Bulk modulus can be thought of as an expansion of Young’s modulus but in all three dimensions, hence the term “bulk.”

Bulk modulus values can be calculated for any material, but it is mostly used to describe the behaviour of fluids (liquids and gases). For anisotropic solids (solids with different properties along different axes), all three moduli are insufficient to predict the behaviour of that material accurately, and so a generalised Hooke’s law is required. There are material-specific formulas that can derive the bulk modulus of the material from its Young’s modulus, shear modulus and Poisson’s ratio.

Bulk modulus is a measure of how compressible a material is, and so the higher the bulk modulus, the lower the compressibility of that material and vice versa. Bulk modulus has the same units as pressure since strain is unitless, and it is often expressed in Pascals, N.m^-2 or PSI.

In this article, you will learn:

• What bulk modulus is
• The measurement of bulk modulus
• Applications of bulk modulus

What is bulk modulus?

Bulk modulus, also known as modulus of compression (denoted as either K or B) is a measurement of a substance’s resistance to isostatic compression [1]. It is the ratio of the infinitesimal change in pressure to the infinitesimal change in volume.

The bulk modulus of a material can be expressed as

`K=-V\frac{\d P}{\d V}`

Where K is the bulk modulus, V is volume and P is pressure.

For ideal isotropic and elastic materials, the bulk modulus, modulus of elasticity, and Poisson’s ratio are related by the following equation [1]:

`K=\frac{E}{3(1-2v)}`

Where K is the bulk modulus, E is the modulus of elasticity, and 𝜈 is Poisson’s ratio. Poisson’s ratio describes the expansion or contraction of a material perpendicular to the applied load.

The bulk modulus of a material is the inverse of its compressibility. So the compressibility of a material is a direct measurement of its bulk modulus. Compressibility c is given by the following equation [2]:

`c=-\frac{1}{V}\frac{\d V}{\d P}`

Changes in the specific gravity (the relative density) and temperature of a liquid can significantly affect its bulk modulus. The bulk modulus of most liquids ranges from 1700 MPa to 2100 MPa, which indicates that in practice most liquids can be considered incompressible, although this is not theoretically true.

Measurement of bulk modulus

The bulk modulus of a material may be measured experimentally through several techniques such as powder diffraction, in which X-rays or electrons are targeted at a powdered or microcrystalline sample. However, more common nowadays are calculated values derived through modelling. These models require input in the form of other tested or known property values in order to produce values for the bulk modulus.

Examples of empirical testing apparatuses for bulk modulus include [3]:

• Vibration Tester
• Acoustic Coupler
• Holographic Interferometer
• Electronic Speckle Pattern Interferometer
• Doppler Interferometer
• Normal Impedance and Flow Ripple Apparatus

Several theoretical formulas have been derived for calculating bulk modulus and, although different, they show good agreement with each other in the values obtained. However, there is little appreciable difference when compared with the experimentally derived values [4].

Below are the three moduli values for selected materials. The bulk modulus of diamond is the highest as it is the hardest known material.

Table 1. The Young’s, bulk and shear moduli of selected materials [5].

Material	Young’s modulus (GPa)	Bulk modulus (GPa)	Shear modulus (GPa)
Aluminium	70	70	30
Bone	15	–	80
Copper	110–120	140	44
Diamond	1120	540	450
Glass	55	31	23
Steel	200	160	84
Tungsten	390–400	200	150
Water	0	2.2	0
Lead	15-17	7.7	5.6

Applications of bulk modulus

Bulk modulus is an important factor to consider in hydraulic systems. The main factors that affect the bulk modulus of a fluid are temperature and entrained (or trapped) gas.

Higher temperatures reduce the bulk modulus, which means the lower the temperature of a fluid, the more difficult it is to compress. Entrained gas, mostly air, dramatically affects the bulk modulus of fluids. The more entrained gas there is in a fluid, the lower the bulk modulus. An exception to this is in the case where the fluid’s bulk modulus is lower than that of air, in which case, the reverse would be the case.

The table below shows how the bulk modulus is affected by varying temperatures and the quantity of entrained air in the hydraulic fluid Brayco 745.

Table 2. The bulk modulus of Brayco 745 at 3000 psi [3].

Entrained Air (%)	Temperature (oF)	Adiabatic Bulk Modulus (psi.)
0	80	268,000
0.1	80	250,000
1	80	149,000
0	180	163,000
1	180	106,000

 

Application for bulk modulus is more critical in fluids than solids because solids are rarely subjected to three-dimensional stress. So the shear and young’s modulus suffice for predicting the behaviour of solids for most applications.

For fluids, the bulk modulus is an essential property that helps especially in the design of hydraulic components such as pumps, cylinders, motors and valves. [3]. Working temperature ranges can be specified and limits set on entrained air to meet design requirements.

For gases, the bulk modulus is vital in the design of sonar (underwater) and echo-location (in air) transducers. 

[1]  M. Biron, “Mechanical Properties,” in Material Selection for Thermoplastic Parts, M. Biron, Ed. William Andrew Publishing, 2016, pp. 261–337.

[2]  J. R. Fanchi, “Fluid Properties,” in Shared Earth Modeling, J. R. Fanchi, Ed. Butterworth-Heinemann, 2002, pp. 87–107.

[3] K. Balasubramanian, “Smart Bulk Modulus Sensor,” M.Sc.. dissertation, Graduate School, Univ. Florida, FL, 2003.

[4] V. A. Greshnyakov and E. A. Belenkov, "Technique for Calculating the Bulk Modulus," Russ. Phys. J., 57, pp. 731–737, 2014.

[5] "Difference between young’s modulus, bulk modulus and shear modulus," PhysicsAbout, March 14, 2020. [Online]. Available: https://physicsabout.com/difference-youngs-modulusbulk-modulus-shear-modulus/ [Accessed May 13, 2020].