Electrical Properties of Materials

If you have traveled internationally, you would have noticed that electrical outlets do not have a standard universal voltage rating - an outlet in the United States is at 110 V while in India, it is 220 V. 

One major reason for this difference is that the United States uses copper for line transmission while India uses cheaper aluminium. In turn, this is a function of a material property called ‘electrical resistivity’ which is higher for aluminium than for copper.

^{An electrical outlet in the US}

In this section, we will explore how different materials react to electrical fields and how these properties are measured. In particular, we will consider the following questions in some detail.

1. What is an electric current? 
2. What is Bandgap?
3. Why are some materials conducting while others are not?
4. What is electrical resistance and conductance?
5. What is specific resistivity and conductivity?
6. What are semiconductors? 
7. What are the breakdown voltage and dielectric strength?
8. What is the temperature coefficient of resistance?
9. What is sheet resistance?
10. What is surface insulation resistance?

Inside a Copper wire

From the outside, a piece of copper wire is a thing of luminescent serenity.

From the inside, it is anything but peaceful. Billions of electrons run around like wild dogs in the space between copper atoms. Like a never-ending bumper cart ride, these electrons constantly collide with each other and the heavy atoms around them. The scene is one of chaos and confusion. 

Most materials do not have electrons in the spaces between atoms. Instead, they have huge interatomic voids that are emptier than outer space.

The electrons in these materials are tightly bound to their atoms and the furthest of them from the center are called valence electrons. These electrons are almost single-handedly responsible for all of Chemistry! 

If you apply just the right amount of energy, these valence electrons can be made to jump from their atoms and into the interatomic void. Liberated from the oppressive electromagnetic pull of the nucleus, they happily roam around the space bumping into atoms and other electrons.

Most materials do not allow their electrons to circulate so freely. The presence of this abundant pool of ‘free’ electrons is unique to metals like copper. 

When the wire is connected to a power supply, these electrons move away from the negative terminal and towards the positive terminal. This flow of electrons is what we commonly refer to as an electric current.

Electric current is the flow of electrons across a material in response to an electric or magnetic field.

Materials like ceramics, plastics, and wood restrict all of their electrons to within the boundary of their atoms. These materials do not have any ‘free’ electrons and hence do not conduct electricity. 

Band Gap

Quantum mechanics teaches us that:

For every material at ambient condition, there is a unique amount of energy required to push a valence electron towards the freedom of interatomic space. This amount of energy is called the Band Gap of the material. 

The bandgap of Diamond, for example, is 5.5 eV. If you apply precisely this amount of energy to a diamond crystal, a single electron will jump from a single carbon atom into the space between atoms. 

Materials such as ceramics have high bandgaps. The Band Gap of silicon dioxide is 9 eV and aluminium nitride is 6 eV. It is relatively hard therefore to create a pool of free electrons in these materials and consequently, they do not conduct electricity. 

Metals like copper have very low band gaps. In fact, they are so low that at room temperature, the energy from ambient heat is sufficient to enable all the valence electrons to break free and run amok inside the metal.

To get some perspective, a centimeter cube of copper has over 8.5 x 10²² free electrons - that is eight-five thousand billion billion electrons!

Thus metals are good conductors of electricity while ceramics, rubber, and wood are bad conductors.

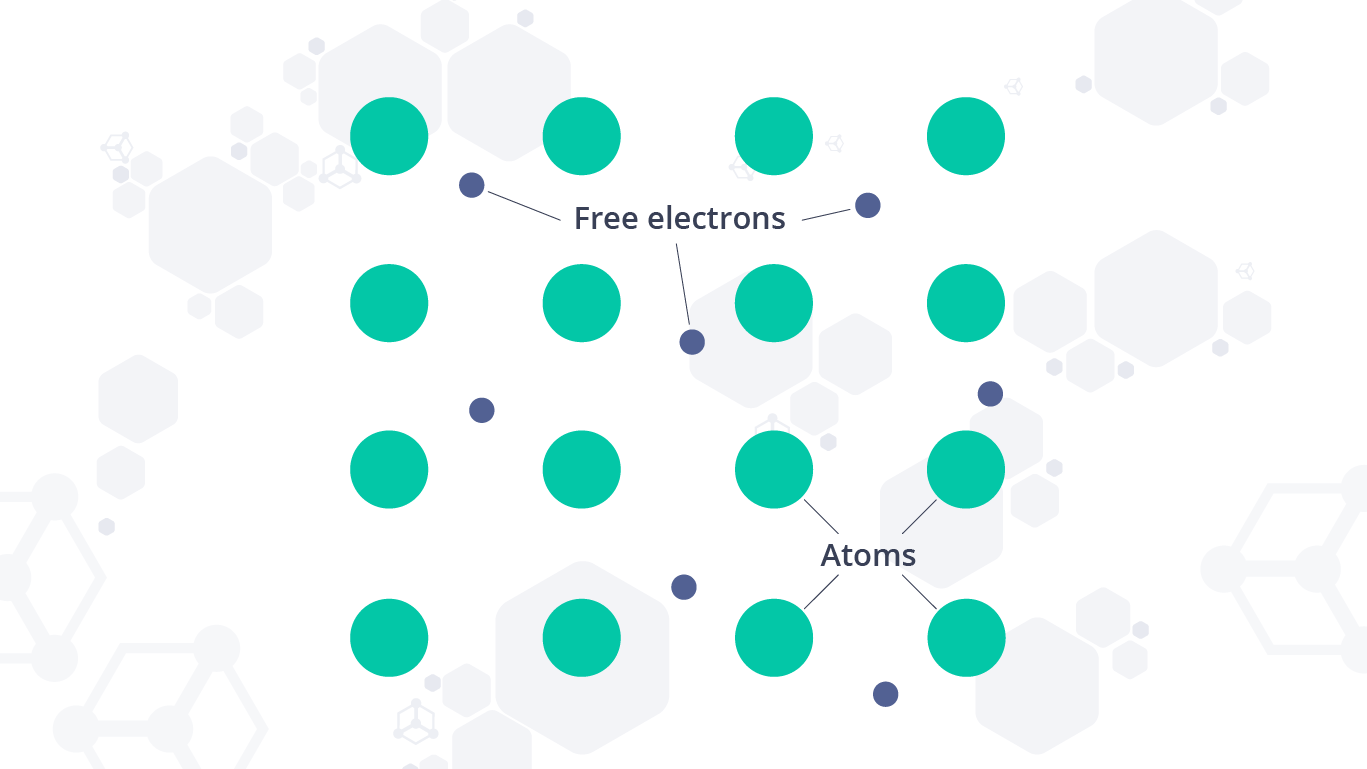
^{Free electrons inside a metal respond to electric fields.}

Conductance and Resistance

To really comprehend the level of chaos inside a metal, we only have to look at the numbers. 

A single electron inside copper at room temperature can theoretically move as fast as 1570 km/s - faster than sound in the air! However, this electron will soon bump into another electron and be kicked in the opposite direction, so that even with enormous speeds, it covers no distance at all. 

So bad is the chaos inside a metal that even with a power supply an electron only manages to cover 23 micrometers in a second - or roughly the diameter of a human hair.

The electron gets thrown off the track so often that the average distance it manages to scrape through is pitiful.

Given this, it might seem like electricity is a very wasteful form of energy transfer - and indeed an argument can be made for this. The real strength of electron flow is in its sheer numbers - even if every electron takes a snalish meandering path in a wire, in billions and billions this results in a powerful transmission of energy.

If electrons moved in steady straight lines, then the effective resistance would be zero.

Simply put, the term resistance is a quantitative measure of the total chaos inside a material.

But how do we quantitatively measure the chaos inside a metal wire? 

Consider two physically identical wires - one made of copper and another of aluminium. We attach the same 12 V battery to each of these wires. 

We can measure the current in them using an electronic measuring device, called a multimeter. 

If the wires have identical diameters and lengths, we should find that the current in the copper wire is higher than that of aluminium. 

Why should this be so? 

For one, copper has far more free electrons than aluminium. 

Aluminium is a smaller atom than copper - its electrons feel the strong attraction of the nucleus and fewer of them escape to be ‘free’. This means in turn, that there are fewer electrons available to transport electric current when compared to copper. 

Thus, for the same voltage, a better conductor will generate a larger current. 

This is formally quantified in what is called as Ohms Law. This law states that:

The current through a conductor between two points is directly proportional to the voltage across the two points.

`V=I\cdot R`

The quantity R is called the resistance of the conductor. Its unit is Volt/ampere usually denoted by ohm (Ω). 

`R=\rho\frac{V}{I}`

The inverse of resistance is called conductance denoted by G. 

`G=\frac{1}{R}=\frac{I}{V}`

Ohm's law was first described by George Ohm in 1827. Interestingly, it was heavily criticised by most scientists and academics at the time. However, it came to be widely accepted in a few decades.

Note that it is incorrect to say that the resistance of aluminium is higher than the resistance of copper. This is because resistance is a function of the physical dimensions of the conductor - such as the length and diameter for a wire. 

Ohm's law is the relationship between current and voltage in ideal resistors.

^{Ohm's law is the relationship between current and voltage in ideal resistors.}

Conductivity and Resistivity

Keeping in mind the wild-dog-chaos theory of electric current that we mentioned earlier, we can deduce that:

1. The longer the length of the wire, the more the chances are for an electron to collide with anything else
2. A large diameter creates more space for electron flow and could decrease the chance of the said collision

These intuitions are mapped mathematically by relating the Resistance (R) to its length (l) and cross-section area (A). 

`R =\rho\frac{l}{A}`

Where rho is a proportionality constant called the resistivity or specific resistivity of a given material. Unlike resistance - which is a macroscopic property, resistivity is a fundamental material property. The unit of resistivity is ohm - meter (Ωm).

`\rho =R\frac{A}{l}`

It is quite common to talk about the inverse of resistivity - a quantity that is appropriately called electrical conductivity or specific conductance denoted by sigma 𝛔. The unit of conductivity is siemens.

`\sigma =\frac{1}{\rho} =\frac{l}{RA}`

The resistivity of copper is 1.68 x 10^-8 Ωm and that of aluminium is 2.65 x 10^-8 Ωm.

As expected, aluminium is more resistive compared to copper, or equivalently, copper is more conductive than aluminium.

Across nature, electrical properties such as resistance and conductivity range over 23 orders of magnitude; i.e. if the smallest value of resistance of any material on earth was 1, the highest value would be 10²³ (ten followed by 23 zeros) times that! No other physical or chemical property shows this kind of variation.

Silver is the best conductor among metals - however, we do not use it for electrical wires because of its prohibitive price. The following table gives the resistivity values of some common materials. It can be seen that the difference between a good conductor such as copper and a bad conductor such as glass can be several orders of magnitude. 

Material	Resistivity (Ωm)
Silver	1.59 x 10-8
Copper	1.68 x 10-8
Silicon	0.1
Dry human skin	1 x 105
Glass	1 x 109
Rubber	1 x 1013

Most nations use copper for transmitting current because it is significantly cheaper than silver.

Semiconductors 

Materials such as silicon and germanium have resistivity values in between that of metals and non-conductors like glass. 

These materials are appropriately called semiconductors. 

What makes these materials interesting is not that they occupy a transitional region from good to bad conductors, but that their conductivity can be easily manipulated. 

By adding a pinch of phosphorus or boron, the conductivity of silicon can be made to go up significantly. Further, each of these 'dopants' leads to two different types of conductivity giving rise to n-type and p-type silicon. 

The electric current in the n and p type is caused by free electrons and positively charged holes, respectively. They behave identically in all other respects. 

Individually and in combination, these materials give rise to all the electronic devices and chips that we know of today.

^{A semiconductor-based electronic device held by a scientist.}

Breakdown Voltage and Dielectric Strength

All semiconductors and other insulators have a maximum voltage that they can withstand. Beyond this voltage, the electric field becomes so high that electrons are pulled from the molecules and atoms causing a large current flow and eventually, failure. 

This maximum voltage that an insulator can withstand is called the breakdown voltage of the material.

The breakdown voltage is also known as dielectric strength if the insulator is a dielectric (solid insulators are called dielectrics). A common application of dielectrics is in an electronic circuit - as resistors, capacitors, inductors etc. The small dimensions of these components mean that they can reach the dielectric strength even with small voltages. Hence, the industrial dielectrics used in these applications need very high dielectric strengths. 

Metals theoretically do not have a breakdown voltage - however, at higher voltages, large current flows can lead to joule heating and subsequent melting of the conductor. 

Temperature Coefficient of Resistance

Resistivity, and consequently resistance, is a function of temperature. Heat can lead to an increase or decrease in resistivity - depending on the material. 

A quantity called the temperature coefficient of resistance (α) quantifies this relationship. It is formally defined as:

The change in resistance divided by the change in temperature for a given quantity of a material is the temperature coefficient of resistance.

`\alpha =\frac{\Delta R}{\Delta T}`

At higher temperature electrons in metals move faster and bump into each other with higher frequency. The resistance of a metal, therefore, increases with temperature (or decrease in conductance). The temperature coefficient of resistance of most metals is therefore positive. 

For semiconductors and nonmetals, an increase in temperature leads to more electrons jumping from atoms to the free space around it. This increase in free electrons causes the conductance of these materials to increase or the resistance to decrease. The temperature coefficient of resistance of semiconductors and non-metals is therefore negative. 

It used to be that we just had two types of conductors - the excellent metals and the pathetic insulators. 

The rise of semiconductors and the associated electronics have made several types of conductors possible. We are today as concerned with the conductivity of thin film of oxide on a substrate as we are about the solder that connects an electric circuit. 

A typical microwave oven, for example, consumes more electricity powering its digital clock than it does heating food.

The unique shapes and sizes of these materials has made it necessary to define several other types of resistivities that might be more suited to the application.

Sheet Resistance

Sheet resistance is mostly defined for a thin film - this is a coating that is usually less than a micrometer thick.

These coatings are widely employed in semiconductors, metal coatings, glass coatings, and resistive pastes. 

Sheet resistance is the resistivity of the material divided by the thickness.

`\rho=R_{s}\cdot t`

In the thin-film industry, some methods such as the four-point probe can directly give the sheet resistance. If the thickness is known, the bulk resistivity of the material can be calculated. 

Surface Insulation Resistance

This is a characteristic of insulating materials used in printed circuit boards that act as contact connectors. Effectively, this is the resistance per unit area of a material under the assumption that the current flows only along the surface. 

Many metallic systems undergo chemical reactions during their operation that can change their conductivity and hence affect the overall performance of the device. 

Surface Insulation resistance enables us to determine the performance of a contact under stress and hence evaluate its suitability for the given application.

^{An electronic circuit with its numerous electrical elements.}